Du réseau au graphe et du graphe au réseau

Qu’ils soient sociaux, naturels ou de transport, les réseaux sont un objet d’étude pour de nombreux chercheurs. Au-delà du concept de réseaux utilisé dans ces disciplines, leurs constructions en soi intéresse les mathématiciens depuis de nombreuses années.

Les réseaux sont ainsi au cœur d’une discipline à part entière : la théorie des graphes du nom de ces modèles composés de sommets (nœuds) et d’arêtes (liens) utilisés pour comprendre l’organisation, le fonctionnement et les propriétés des réseaux qui en découlent.

Il est passé par ici, il repassera par là…

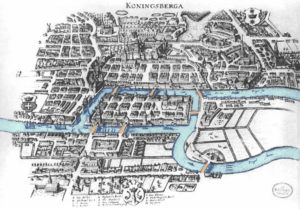
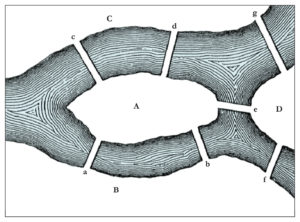
C’est Leonhard Euler le premier qui a théorisé avec des graphes, en étudiant le problème des 7 ponts de Königsberg. Dans cette ville, bâtie autour de 2 îles reliées entre elles par 1 pont et au reste de la ville par 6 autres ponts, comment est-il possible de cheminer en passant sur tous les ponts et revenir à son point de départ sans repasser deux fois sur le même ?

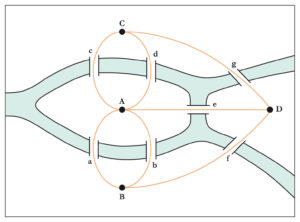
La solution donnée par Euler grâce à un graphe à 4 sommets et 7 arêtes est que c’est impossible ! Pour que ça marche il eut fallu que le nombre d’arêtes reliant chaque île ou rive soit pair.

Sommets bariolés

Les applications de ces théories des graphes sont nombreuses dans les recherches sur les réseaux routiers, de communication ou informatiques. Par exemple, la coloration des sommets (dont le principe est d’attribuer une couleur à chaque sommet d’un graphe de manière à ce que deux sommets reliés par une arête ne soient jamais de la même couleur et en utilisant le moins de couleurs possible) est utilisée pour attribuer les fréquences dans les réseaux de  télécommunication sans fil afin que deux émetteurs à proximité ne se parasitent pas en émettant à la même fréquence. Quand il n’y a que 5 sommets dans le graphe c’est relativement aisé, en revanche quand le nombre de sommets et la configuration du graphe évoluent, ça se corse.